Порядок разностного уравнения. Линейные разностные уравнения с постоянными коэффициентами. с постоянными коэффициентами

РАЗНОСТНЫЕ УРАВНЕНИЯ - уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, ..., xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени.

Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность

y = y(t+1) – y(t),

которую часто называют первой разностью. При этом различают правую и левую разности, в частности

y = y(t) – y(t–1)

Левая, а приведенная выше - правая. Можно определить вторую разность:

Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) –

– 2y(t + 1) + y(t)

и разности высших порядков Δn.

Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке:

f = 0.

Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек

y(t), y(t+1), ..., y(t+n).

При этом разность между последним и первым моментами времени называется порядком уравнения.

При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю.

При исследовании функций многих переменных по аналогии с частными производными (см. Производная) вводятся также частные разности.

Линейные разностные уравнения первого порядка

y(x + 1) − ay(x) = 0. Линейное однородное разностное уравнение первого порядка с постоянными коэффициентами.

y(x + 1) − ay(x) = f(x). Линейное неоднородное разностное уравнение первого порядка с постоянными коэффициентами.

y(x + 1) − xy(x) = 0.

y(x + 1) − a(x − b)(x − c)y(x) = 0.

y(x + 1) − R(x)y(x) = 0, где R(x) -- рациональная функция.

y(x + 1) − f(x)y(x) = 0.

y(x + a) − by(x) = 0.

y(x + a) − by(x) = f(x).

y(x + a) − bxy(x) = 0.

y(x + a) − f(x)y(x) = 0.

Линейные разностные уравнения второго порядка, yn = y(n)

yn+2 + ayn+1 + byn = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.

yn+2 + ayn+1 + byn = fn. Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + ay(x + 1) + by(x) = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + ay(x + 1) + by(x) = f(x). Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + a(x + 1)y(x + 1) + bx(x + 1)y(x) = 0.

Р а з н о с т н ы м у р а в н е н и е м наз. уравнение вида

где - искомая и F - заданная функции. Замена в (2) конечных разностей их выражениями через значения искомой функции согласно (1) приводит к уравнению вида

Если , т. е. уравнение (3) действительно содержит как , так и , то уравне-вие (3) наз. р а з н о с т н ы м у р а в н е н и е м m-го п о р я д к а, или д и ф ф е р е н ц и а л ь н о-р а з н о с т н ы м у р а в н е н и е м.

(6)

где - произвольные постоянные.

3) Общее решение неоднородного Р. у. (4) представляется в виде суммы какого-либо частного его решения и общего решения однородного Р. у. (5).

Частное решение неоднородного уравнения (5) можно построить, исходя из общего решения (6) однородного уравнения, путем применения метода вариации произвольных постоянных (см., напр., ). В случае Р. у. с постоянными коэффициентами

можно непосредственно найти тлинейно независимых частных решений. Для этого рассматривается харак-теристич. уравнение

и ищутся его корни . Если все корни простые, то функции

образуют линейно независимую систему решений уравнения (7). В случае, когда - корень кратности r, линейно независимыми являются решения

Если коэффициенты а 0 , a 1 , . . ., а т действительные и уравнение (8) имеет комплексный корень, напр. простой корень , то вместо комплексных решений выделяют два линейно независимых действительных решения

Пусть имеется Р. у. 2-го порядка с постоянными действительными коэффициентами

(9) Характеристич. уравнение

имеет корни

Общее решение уравнения (9) в случае удобно записывать в виде

(10)

где с 1 и с 2 - произвольные постоянные. Если и - комплексно сопряженные корни:

то другое представление общего решения имеет вид

В случае кратного корня общее решение может быть получено предельным переходом из (10) или (11). Оно имеет вид

Как и в случае уравнений произвольного порядка, для Р. у. 2-го порядка можно рассматривать задачу Коши или различные краевые задачи. Напр., для задачи Коши

Решение обыкновенных линейных разностных уравнений

с постоянными коэффициентами

Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами

,

где y[ n] - выходной сигнал в момент n ,

x[ n] - входной сигнал в момент n ,

a i , b k – постоянные коэффициенты.

Для решения таких уравнений могут использоваться два метода

• Прямой метод,
• Метод Z – преобразования.

Вначале рассмотрим решение линейного разностного уравнения с помощью прямого метода.

Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения

Общее решение однородного разностного уравнения (zero- input response ) y h [ n]

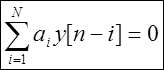
определяется в виде

.

Подставляя это решение в однородное уравнение, получаем

Такой полином называют характеристическим полиномом системы. Он имеет N корней . Корни могут быть действительными или комплексными и некоторые корни - совпадающими (кратными).

Если корни являются действительными и разными, то решение однородного уравнения имеет вид

где коэффициенты

Если некоторый корень, например, λ 1 имеет кратность m , то соответствующий ему член решения приобретает форму

Если все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням можно представить (записать) в виде , при этом коэффициенты A, B определяются по начальным условиям.

Вид частного решения y p [ n] уравнения зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице

Таблица 1. Вид частного решения для различного характера правой части

Входной сигнал x[n]	Частное решение y p [n]
A (константа)

Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности и временного сдвига. В результате получается линейное алгебраическое уравнение относительно Z - изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.

Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.

Пример . Определим отклик (выходной сигнал) системы, описываемой линейным разностным уравнением , на входной сигнал

Решение .

1. Прямой метод решения уравнения.

Однородное уравнение . Его характеристический полином .

Корни полинома .

Решение однородного уравнения .

Поскольку,то частное решение определяем в виде .

Подставляем его в уравнение

Для нахождения константы К примем n = 2 . Тогда

Или , К=2,33

Отсюда частное решение и общее решение разностного уравнения (1)

Найдем константы С 1 и С 2 . Для этого положим n = 0 , тогда из исходного разностного уравнения получаем . Для данного уравнения

Поэтому . Из выражения (1)

Следовательно,

.

Из выражения (1) для n = 1 имеем .
Получаем следующие два уравнения для С 1 и С 2

.

Решение этой системы дает следующие значения: С 1 =0,486 и С 2 = -0,816.

Следовательно, общее решение данного уравнения

2. Решение методом Z – преобразования.

Возьмем Z – преобразование от исходного разностного уравнения , учитывая свойство (теорему) временного сдвига . Получаем

На практике простейшие разностные уравнения возникают при исследовании например величины банковского вклада. Эта величина является переменной Y x , представляющей сумму, которая накапливается по установленному закону при целочисленных значениях аргумента x . Пусть сумма Y o положена в банк при условии начисления 100 r сложных процентов в год. Пусть начисление процентов производится один раз в год и x обозначает число лет с момента помещения вклада (x = 0, 1, 2,...). Обозначим величину вклада по истечении x лет через Y x . Мы получаем

Y x = (1+r)Y x-1.

Если начальная сумма составляет Y o , мы приходим к задаче отыскания решения полученного разностного уравнения, подчиненного начальному условию Y x = Y o при x = 0. Полученное разностное уравнение содержит Y x и значение этой переменной на один год раньше, т.е. Y x-1; в данном случае аргумент x явно не входит в разностное уравнение.

Вообще говоря, обыкновенное разностное уравнение устанавливает связь между значениями функции Y = Y(x ), рассматриваемой для ряда равноотстоящих значений аргумента x , но можно без ограничения общности считать, что искомая функция определена для равноотстоящих значений аргумента с шагом, равным единице. Таким образом, если начальное значение аргумента есть x , то ряд его равноотстоящих значений будет x , x+1, x+2,... и в обратном направлении: x , x-1, x-2,.... Соответствующие значения функции будем обозначать Y x, Y x+1, Y x+2, ... или Y x , Y x-1, Y x-2, .... Определим так называемые разности различных порядков функции Y x с помощью следующих формул:

Разности первого порядка

D Y x = Y x+1 - Y x ,

D Y x+1 =Y x+2 - Y x+1,

D Y x+2 = Y x+3 - Y x+2,

... ... ... ... ...

Разности второго порядка

D 2 Y x = D Y x+1 - D Y x ,

D 2 Y x+1 = D Y x+2 - D Y x+1 ,

D 2 Y x+2 = D Y x+3 - D Y x+2 ,

... ... ... ... ...

Разности третьего порядка

D 3 Y x = D 2 Y x+1 - D 2 Y x ,

D 3 Y x+1 = D 2 Y x+2 - D 2 Y x+1 ,

... ... ... ... ...

Обыкновенным разностным уравнением называется уравнение, связывающее значения одного независимого аргумента x , его функцииY x и разностей различных порядков этой функции D Y x , D 2 Y x, D 3 Y x, .... Такое уравнение можно записать в общем виде следующим образом:

j (x , Y x , D Y x , D 2 Y x D 3 Y x , D n Y x ) = 0, (10.1)

которое по форме аналогично дифференциальному уравнению.

Порядком разностного уравнения называется порядок наивысшей разности, входящей в это уравнение. Разностное уравнение (10.1) часто удобнее записать, пользуясь не разностями неизвестной функции, а ее значениями при последовательных значениях аргумента, то есть выразить D Y x , D 2 Y x, D 3 Y x ,... через Y x , Y x+1 , Y x+2, .... Уравнение (10.1) можно привести к одной из двух форм:

y (x , Y x , Y x+1, ...,Y x+n ) = 0, (10.2)

x (x , Y x , Y x-1, ...,Y x -n) = 0. (10.3)

Общее дискретное решение Y x обыкновенного разностного уравнения n -го порядка представляет функцию x (x = 0, 1. 2,...), содержащую ровно n произвольных постоянных:

Y x = Y(x, C 1 , C 2 ,..., C n ).

Паутинообразная модель

Пусть рынок какого-либо отдельного товара характеризуется следующими функциями спроса и предложения:

D = D(P), S = S(P).

Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан, или

D( P) = S(P).

Цена равновесия задается этим уравнением (которое может иметь множество решений), а соответствующий объем покупок-продаж, обозначаемый через , - следующим уравнением:

D () = S( ).

Динамическая модель получается при наличии запаздывания спроса или предложения. Простейшая модель в дискретном анализе включает неизменное запаздывание или отставание предложения на один интервал:

D t = D (P t) и S t = S (P t-1).

Это может случиться, если для производства рассматриваемого товара требуется определенный период времени, выбранный за интервал. Действие модели таково: при заданном P t-1 предшествующего периода объем предложения на рынке в текущем периоде будет S (P t-1), и величина P t должна установиться так, чтобы был куплен весь объем предложенного товара. Иными словами, P t и объем покупок-продаж X t характеризуются уравнением:

X t = D (P t) = S (P t-1).

Итак, зная исходную цену P o , с помощью этих уравнений мы можем получить значения P 1 и X 1. Затем, используя имеющуюся цену P 1, из соответствующих уравнений получим значения P 2 и X 2 и т.д. В общем изменение P t характеризуется разностным уравнением первого порядка (одноинтер­вальное отставание):

D (P t) = S (P t-1).

Решение можно проиллюстрировать диаграммой, представленной на рис.5, где D и S - соответственно кривые спроса и предложения, а положение равновесия (со значениями и ) соответствует точке их пересечения Q. Цена в начальный момент времени равна P o . Соответствующая точка Q o на кривой S дает объем предложения в период 1. Весь этот предложенный объем товара раскупается при цене P 1 , заданной точкой Q 1 на кривой D с той же ординатой (X 1), что и Q o . Во второй период времени движение происходит сначала по вертикали от точки Q 1 к точке на кривой S, дающей X 2, а затем по горизонтали - к точке Q 2 на кривой D. Последняя точка характеризует P 2 . Продолжение этого процесса и дает график паутины , показанный на рис. 5. Цены и объемы (покупок - продаж) в последовательные периоды времени являются соответственно координатами точек Q 1 , Q 2 , Q 3 ,... на кривой спроса D. В рассматриваемом случае последовательность точек стремится к Q. При этом точки поочередно располагаются на левой и правой стороне от Q. Следовательно, и значения цены P t стремятся к , располагаясь поочередно по обе стороны от . Точно так же обстоит дело и с объемами покупок - продаж (X t ).

Решение можно получить алгебраически для случая линейных функций спроса и предложения: D = a +aP , S = b +bP . Значения равновесия и будут заданы уравнениями

A +a = b +b ,

то есть

= (a - b )/(b - a), = (b a - a b )/(b - a). (10.4) . р t-1. (10.7)

Уравнения (10.7) аналогичны (10.5), за исключением того, что они описывают отклонения от уровней равновесия (теперь уже известно, что таковые существуют). Оба эти уравнения являются разностными уравнениями первого порядка. Положим c = b /a и подставим его в уравнение (10.7), так что разностное уравнение относительно р t будет

р t = c р t-1 . (10.8)

При данном значении р o в момент t = 0 из (10.8) получаем решение:

р t = р o c t,

или

P t = + (P o - ) c t .

Введение

В последние десятилетия математические методы всё настойчивее проникают в гуманитарные науки и в частности, в экономику. Благодаря математике и её эффективному применению можно надеяться на экономический рост и процветание государства. Эффективное, оптимальное развитие невозможно без использования математики.

Целью данной работы является изучение применения разностных уравнений в экономической сфере общества.

Перед данной работой ставятся следующие задачи: определение понятия разностных уравнений; рассмотрение линейных разностных уравнений первого и второго порядка и их применение в экономике.

При работе над курсовым проектом были использованы доступные для изучения материалы учебных пособий по экономике, математическому анализу, работы ведущих экономистов и математиков, справочные издания, научные и аналитические статьи, опубликованные в Интернет - изданиях.

Разностные уравнения

§1. Основные понятия и примеры разностных уравнений

Разностные уравнения играют большую роль в экономической теории. Многие экономические законы доказывают с помощью именно этих уравнений. Разберем основные понятия разностных уравнений.

Пусть время t выступает как независимая переменная, а зависимая переменная определяется для времени t, t-1, t-2 и т.д.

Обозначим через значение в момент времени t; через - значение функции в момент, сдвинутый назад на единицу (например, в предыдущем часу, на предыдущей неделе и т.д.); через - значение функции y в момент, сдвинутый на две единицы назад, и т.д.

Уравнение

где - постоянные, называется разностным неоднородным уравнением n-го порядка с постоянными коэффициентами.

Уравнение

В котором =0, называется разностным однородным уравнением n-го порядка с постоянными коэффициентами. Решить разностное уравнение n-го порядка - значит найти функцию, которая обращает это уравнение в верное тождество.

Решение, в котором отсутствует произвольная постоянная, называется частным решением разностного уравнения; если же в решении есть произвольная постоянная, то оно называется общим решением. Можно доказать следующие теоремы.

Теорема 1. Если однородное разностное уравнение (2) имеет решения и, то решением будет также функция

где и - произвольные постоянные.

Теорема 2. Если - частное решение неоднородного разностного уравнения (1) и - общее решение однородного уравнения (2), то общим решением неоднородного уравнения (1) будет функция

Произвольные постоянные. Эти теоремы сходны с теоремами для дифференциальных уравнений. Системой линейных разностных уравнений первого порядка с постоянными коэффициентами называется система вида

где - вектор из неизвестных функций, - вектор из известных функций.

Есть матрица размера nn.

Эта система может быть решена сведением к разностному уравнению n-го порядка по аналогии с решением системы дифференциальных уравнений.

§ 2. Решение разностных уравнений

Решение разностного уравнения первого порядка. Рассмотрим неоднородное разностное уравнение

Соответствующее однородное уравнение есть

Проверим, будет ли функция

решением уравнения (3).

Подставляя в уравнение (4), получаем

Следовательно, есть решение уравнения (4).

Общее решение уравнения (4) есть функция

где C - произвольная постоянная.

Пусть - частное решение неоднородного уравнения (3). Тогда общее решение разностного уравнения (3) есть функция

Найдем частное решение разностного уравнения (3), если f(t)=c, где c - некоторая переменная.

Будем искать решение в виде постоянной m. Имеем

Подставив эти постоянные в уравнение

получаем

Следовательно, общее решение разностного уравнения

Пример1 . Найти с помощью разностного уравнения формулу прироста денежного вклада А в сбербанке, положенного под p % годовых.

Решение . Если некоторая сумма положена в банк под сложный процент p, то к концу года t её размер составит

Это однородное разностное уравнение первого порядка. Его решение

где C - некоторая постоянная, которую можно рассчитать по начальным условиям.

Если принять, то C=A, откуда

Это известная формула подсчета прироста денежного вклада, положенного в сбербанк под сложный процент.

Решение разностного уравнения второго порядка. Рассмотрим неоднородное разностное уравнение второго порядка

и соответствующее однородное уравнение

Если k является корнем уравнения

есть решение однородного уравнения (6).

Действительно, подставляя в левую часть уравнения (6) и учитывая (7), получаем

Таким образом, если k - корень уравнения (7), то - решение уравнения (6). Уравнение (7) называется характеристическим уравнением для уравнения (6). Если дискриминант характеристическое уравнение (7) больше нуля, то уравнение (7) имеет два разных действительных корня и, а общее решение однородного уравнения (6) имеет следующий вид.